728x90
백준 2042 - 구간 합 구하기
https://www.acmicpc.net/problem/2042

문제
어떤 N개의 수가 주어져 있음/ 중간에 수의 변경이 빈번히 일어나고 그 중간에 어떤 부분의 합을 구하려고 함
ex. 1, 2, 3, 4, 5 -> 3번째 수를 6으로 바꾸고 2 ~ 5까지의 합 => 17
입력
첫째 줄: 수의 개수 N (1 <= N <= 1,000,000)
, 수의 변경이 일어나는 횟수 M (1 <= M <= 10,000), 구간의 합을 구하는 횟수 K (1 <= K <= 10,000)
둘째 줄 ~ N + 1번째 줄: N개의 수
N + 2번째 줄 ~ N + M + K + 1번째 줄: 세 개의 정수 a, b, c
a가 1인 경우 b번째 수를 c로 바꾸고 a가 2인 경우에는 b번째 수부터 c번째 수까지의 합 구하여 출력
(1 <= b <= N, b <= c <= N)
출력: 첫째 줄부터 K줄에 걸쳐 구한 구간의 합 출력 ($-2^{63}$ <= 답 <= $-2^{63} - 1$)
풀이
세그먼트 트리(Segment Tree)
- 배열의 구간 정보를 빠르게 처리하기 위한 트리 자료구조
- 시간 복잡도: O(log N)
- ex. 구간 합, 구간 최소/최댓값, 구간 곲, XOR, AND 등, 값 변경(update), 구간 질의(query)
IF. N <= 1,000,000 / 쿼리 M <= 100,000 / 매 쿼리마다 구간 [l, r]의 합 구하기
- 단순 배열: 한 번 구할 때 O(N) => 전체 O(NM)
- 누적합: 구간 합은 빠르지만, 값 변경 나오면 전체 다시 계산
- 세그먼트 트리: 구간 합 O(log N) / 값 변경 O(log N)
이진 트리
- 리프 노드: 배열의 실제 값
- 내부 노드: 자식 노드들의 결과를 합친 값
- 합 문제 -> 합 / 최소 문제 -> min / 최대 문제 -> max
핵심 연산
- ini (트리 생성): 배열 기반으로 트리 한 번 만듦 / O(N)
- query (구간 질의): 현재 노드의 구간이
- 완전히 벗어나면 -> 무시
- 완전히 포함되면 -> 바로 사용
- 일부만 겹치면 -> 자식으로 내려감
- => 트리 높이만큼만 이동: O(log N)
- update (값 변경): 바뀐 값이 포함된 구간만 갱신 / 루프 -> 리프까지 내려가며 수정 / O(log N)
*메모리: 약 4N
트리 생성: `arr` 배열 기반으로 세그먼트 트리 한 번 만들어두는 함수
- `arr = new long[N + 1]`: 실제 배열 값
- `tree = new long[4 * N]`: 세그먼트 트리 -> 구간 합 저장
- 리프 노드: `start == end`: 하나의 원소만 담당 -> 그대로 저장
- 내부 노드: `tree[node] = tree[node * 2] + tree[node * 2 + 1]`: 왼쪽 구간 + 오른쪽 구간 합
static void init(int node, int start, int end) {
if (start == end) {
tree[node] = arr[start];
return;
}
int mid = (start + end) / 2;
init(node * 2, start, mid);
init(node * 2 + 1, mid + 1, end);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
값 변경: `idx` 위치의 값이 `diff`만큼 변했을 때 해당 값을 포함하는 모든 구간에 반영
- `idx < start || idx > end`: 현재 구간에 `idx 없음 => 무시
- `start != end`: 리프 X => 자식으로 계속 내려감
static void update(int node, int start, int end, int idx, long diff) {
if (idx < start || idx > end) return;
tree[node] += diff;
if (start != end) {
int mid = (start + end) / 2;
update(node * 2, start, mid, idx, diff);
update(node * 2 + 1, mid + 1, end, idx, diff);
}
}
query: 구간 [lt, rt] 합
- 완전히 벗어남: `rt < start || end < lt`
- 완전히 포함: `lt <= start && end <= rt`
- 일부만 겹침: `return query(lt) + query(rt)`
static long query(int node, int start, int end, int lt, int rt) {
if (rt < start || end < lt) return 0;
if (lt <= start && end <= rt) return tree[node];
int mid = (start + end) / 2;
return query(node * 2, start, mid, lt, rt)
+ query(node * 2 + 1, mid + 1, end, lt, rt);
}코드
import java.io.*;
import java.util.*;
// 구간 합 구하기
public class boj_2042 {
static int N, M, K;
static long[] arr;
static long[] tree;
static void init(int node, int start, int end) {
if (start == end) {
tree[node] = arr[start];
return;
}
int mid = (start + end) / 2;
init(node * 2, start, mid);
init(node * 2 + 1, mid + 1, end);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
static void update(int node, int start, int end, int idx, long diff) {
if (idx < start || idx > end) return;
tree[node] += diff;
if (start != end) {
int mid = (start + end) / 2;
update(node * 2, start, mid, idx, diff);
update(node * 2 + 1, mid + 1, end, idx, diff);
}
}
static long query(int node, int start, int end, int lt, int rt) {
if (rt < start || end < lt) return 0;
if (lt <= start && end <= rt) return tree[node];
int mid = (start + end) / 2;
return query(node * 2, start, mid, lt, rt)
+ query(node * 2 + 1, mid + 1, end, lt, rt);
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
arr = new long[N + 1];
tree = new long[4 * N];
for (int i = 1; i <= N; i++) {
arr[i] = Long.parseLong(br.readLine());
}
init(1, 1, N);
for (int i = 0; i < M + K; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
long c = Long.parseLong(st.nextToken());
if (a == 1) {
long diff = c - arr[b];
arr[b] = c;
update(1, 1, N, b, diff);
} else {
sb.append(query(1, 1, N, b, (int) c)).append('\n');
}
}
System.out.println(sb);
}
}백준 10999 - 구간 합 구하기 2
https://www.acmicpc.net/problem/10999
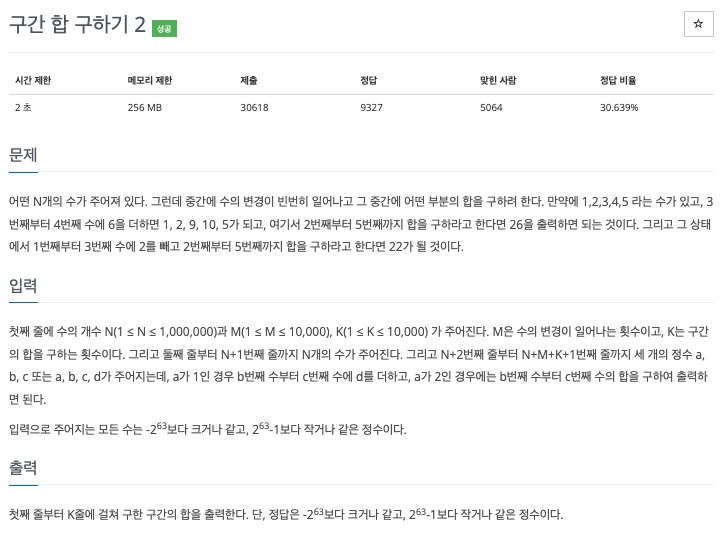
문제
어떤 N개의 수가 주어져 있음/ 중간에 수의 변경이 빈번히 일어나고 그 중간에 어떤 부분의 합을 구하려고 함
ex. 1, 2, 3, 4, 5
-> 3번째부터 4번째 수에 6 더하면 1, 2, 9, 10, 5/ 2번째부터 5번째 합 => 26
-> 1번째부터 3번째 수에 2를 빼고 2번째부터 5번째 합 => 22
입력
첫째 줄: 수의 개수 N (1 <= N <= 1,000,000)
, 수의 변경이 일어나는 횟수 M (1 <= M <= 10,000), 구간의 합을 구하는 횟수 K (1 <= K <= 10,000)
둘째 줄 ~ N + 1번째 줄: N개의 수
N + 2번째 줄 ~ N + M + K + 1번째 줄: 세 개의 정수 a, b, c
a가 1인 경우 b번째 수부터 c번째 수에 d를 더하고, a가 2인 경우에는 b번째 수부터 c번째 수까지의 합 구하여 출력
(1 <= b <= N, b <= c <= N)
출력: 첫째 줄부터 K줄에 걸쳐 구한 구간의 합 출력 ($-2^{63}$ <= 답 <= $-2^{63} - 1$)
풀이
static void propagate(int node, int start, int end) {
if (lazy[node] != 0) {
tree[node] += (end - start + 1) * lazy[node];
if (start != end) {
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
}
static void update(int node, int start, int end, int lt, int rt, long diff) {
propagate(node, start, end);
if (rt < start || end < lt) return;
if (lt <= start && end <= rt) {
lazy[node] += diff;
propagate(node, start, end);
return;
}
tree[node] += diff;
int mid = (start + end) / 2;
update(node * 2, start, mid, lt, rt, diff);
update(node * 2 + 1, mid + 1, end, lt, rt, diff);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
static long query(int node, int start, int end, int lt, int rt) {
propagate(node, start, end);
if (rt < start || end < lt) return 0;
if (lt <= start && end <= rt) return tree[node];
int mid = (start + end) / 2;
return query(node * 2, start, mid, lt, rt)
+ query(node * 2 + 1, mid + 1, end, lt, rt);
}코드
import java.io.*;
import java.util.*;
// 구간 합 구하기 2
public class boj_10999 {
static int N, M, K;
static long[] arr, tree, lazy;
static void init(int node, int start, int end) {
if (start == end) {
tree[node] = arr[start];
return;
}
int mid = (start + end) / 2;
init(node * 2, start, mid);
init(node * 2 + 1, mid + 1, end);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
static void propagate(int node, int start, int end) {
if (lazy[node] != 0) {
tree[node] += (end - start + 1) * lazy[node];
if (start != end) {
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
}
static void update(int node, int start, int end, int lt, int rt, long diff) {
propagate(node, start, end);
if (rt < start || end < lt) return;
if (lt <= start && end <= rt) {
lazy[node] += diff;
propagate(node, start, end);
return;
}
tree[node] += diff;
int mid = (start + end) / 2;
update(node * 2, start, mid, lt, rt, diff);
update(node * 2 + 1, mid + 1, end, lt, rt, diff);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
static long query(int node, int start, int end, int lt, int rt) {
propagate(node, start, end);
if (rt < start || end < lt) return 0;
if (lt <= start && end <= rt) return tree[node];
int mid = (start + end) / 2;
return query(node * 2, start, mid, lt, rt)
+ query(node * 2 + 1, mid + 1, end, lt, rt);
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
arr = new long[N + 1];
tree = new long[4 * N];
lazy = new long[4 * N];
for (int i = 1; i <= N; i++) {
arr[i] = Long.parseLong(br.readLine());
}
init(1, 1, N);
for (int i = 0; i < M + K; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
if (a == 1) {
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
long d = Long.parseLong(st.nextToken());
update(1, 1, N, b, c, d);
} else {
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
sb.append(query(1, 1, N, b, c)).append('\n');
}
}
System.out.println(sb);
}
}728x90
반응형
'✏️ > BOJ' 카테고리의 다른 글
| [BOJ/DP] 백준 11066 - 파일 합치기 (Java) (0) | 2025.12.22 |
|---|---|
| [BOJ/DP] 백준 11049 - 행렬 곱셈 순서 (Java) (0) | 2025.12.22 |
| [BOJ/Greedy] 백준 1700 - 멀티탭 스케줄링 (Java) (0) | 2025.12.16 |
| [BOJ] 백준 1516 - 게임 개발 (Java) (0) | 2025.12.15 |
| [BOJ] 백준 6549 - 히스토그램에서 가장 큰 직사각형 (Java) (0) | 2025.12.14 |
