[이것이 취업을 위한 코딩 테스트다 with 파이썬] 7. 최단 경로 알고리즘

최단 경로 알고리즘

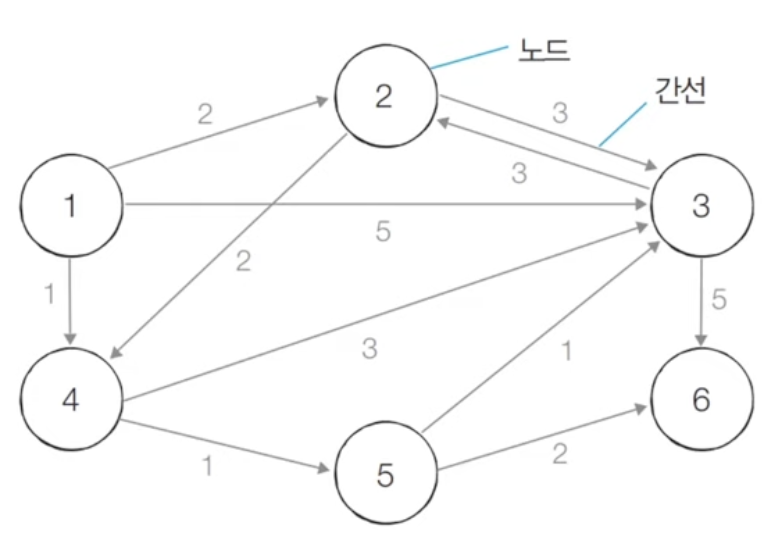
• 가장 짧은 경로를 찾는 알고리즘 
• 다양한 문제 상황
  • 한 지점에서 다른 한 지점까지의 최단 경로
  • 한  지점에서 다른 모든 지점까지의 최단 경로
  • 모든 지점에서 다른 모든 지점까지의 최단 경로
• 각 지점 -> 그래프에서 노드로 표현
• 지점 간 연결된 도로 -> 그래프에서 간선으로 표현

---

다익스트라 최단 경로 알고리즘

• 특정한 노드에서 출발하여 다른 모든 노드로 가는 최단 경로를 계산
• 음의 간선이 없을 때 정상적으로 동작
  • 현실 세계의 도로(간선) -> 음의 간선으로 표현 X
• 그리디 알고리즘으로 분류
  • 매 상황에서 가장 비용이 적은 노드를 선택해 임의의 과정 반복

동작 과정

1. 출발 노드 설정
2. 최단 거리 테이블 초기화
3. 방문 X 노드 중에서 최단 거리가 가장 짧은 노드 선택
4. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산 -> 최단 거리 테이블 갱신
5. 3번과 4번 반복ㅅ음

• 알고리즘 동작 과정에서 최단 거리 테이블 -> 각 노드에 대한 현재까지의 최단 거리 정보 가지고 있음
• 처리 과정에서 더 짧은 경로 찾으면 갱신

특징

• 그리디 알고리즘: 매 상황에서 방문 X 가장 비용이 적은 노드를 선택해 임의의 과정 반복
• 단계 거치며 한 번 처리된 노드의 최단 거리는 고정 -> 더 이상 바뀌지 X
  • 한 단계당 하나의 노드에 대한 최단 거리를 확실히 찾는 것으로 이해할 수 있음
• 다익스트라 알고리즘을 수행한 뒤에 테이블에 각 노드까지의 최단 거리 정보가 저장
  • 완벽한 형태의 최단 경로 구하려면 소스코드에 추가적인 기능 더 넣어야 함

구현 방법

단계마다 방문 X 노드 중 최단 거리가 가장 짧은 노드를 선택 

-> 매 단계마다 1차원 테이블의 모든 원소를 확인(순차 탐색)

성능 분석

• 총 O(V)번에 걸쳐서 최단 거리가 가장 짧은 노드를 매번 선형 탐색해야 함
• => 전체 시간 복잡도 $O(V^2)$
• 일반적으로 코딩 테스트의 최단 경로 문제에서 전체 노드의 개수 <= 5,000개 -> 이 코드로 문제 해결

Python

import sys
input = sys.stdin.realine
INF = int(1e9) # 무한을 의미하는 값(10억)

# 노드의 개수, 간선의 개수를 입력받기
n, m = map(int, input().split())
# 시작 노드 번호를 입력받기
start = int(input())
# 각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트를 만들기
graph = [[] for i in range(n + 1)]
# 방문한 적이 있는지 체크하는 목적의 리스트를 만들기
visited = [False] * (n + 1)
# 최단 거리 테이블 -> 모두 무한으로 초기화
distance = [INF] * (n + 1)

# 모든 간선 정보를 입력받기
for _ in range(m):
    a, b, c = map(int, input().split())
    # a번 노드에서 b번 노드로 가는 비용이 c라는 의미
    graph[a].append((b, c))

# 방문 X 노드 중에서, 가장 최단 거리가 짧은 노드의 번호를 반환
def get_smallest_node():
    min_value = INF
    index = 0 # 가장 최단 거리가 짧은 노드(인덱스)
    for i in range(1, n + 1):
        if distance[i] < min_value and not visited[i]:
            min_value = distance[i]
            index = i
    return index

def dijkstra(start):
    # 시작 노드에 대해서 초기화
    distance[start] = 0
    visited[start] = True
    for j in graph[start]:
        distance[j[0]] = j[1]
    # 시작 노드를 제외한 전체 n - 1개의 노드에 대해 반복
    for i in range(n - 1):
        # 현재 최단 거리가 가장 짧은 노드를 꺼내서, 방문 처리
        now = get_smallest_node()
        visited[now] = True
        # 현재 노드와 연결된 다른 노드를 확인
        for j in graph[now]:
            cost = distance[now] + j[1]
            # 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
            if cost < distance[j[0]]:
                distance[j[0]] = cost

# 다익스트라 알고리즘을 수행
dijkstra(start)

# 모든 노드로 가기 위한 최단 거리를 출력
for i in range(1, n + 1):
    # 도달할 수 X 경우 -> 무한(INFINITY) 출력
    if distance[i] == INF:
        print("INFINITY")
    # 도달할 수 O 경우 -> 거리 출력
    else:
        print(distance[i])

C++

#include <bits/stdc++.h>
#define INF 1e9 // 무한을 의미하는 값(10억)
using namespace std;

// 노드의 개수(N), 간선의 개수(M), 시작 노드 번호(Start)
// 노드의 개수: 최대 100,000개 가정
int n, m, start;
// 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열
vector<pair<int, int> > graph[100001];
// 방문한 적이 있는지 체크하는 목적의 배열 만들기
bool visited[100001];
// 최단 거리 테이블 만들기
int d[100001];

// 방문 X 노드 중에서, 가장 최단 거리가 짧은 노드의 번호를 반환
int getSmallestNode() {
    int min_value = INF;
    int index = 0; // 가장 최단 거리가 짧은 노드(인덱스)
    for (int i = 1; i <= n; i++) {
        if (d[i] < min_value && !visited[i]) {
            min_value = d[i];
            index = i;
        }
    }
    return index;
}

void dijkstra(int start) {
    // 시작 노드에 대해서 초기화
    d[start] = 0;
    visited[start] = true;
    for (int j = 0; j < graph[start].size(); j++) {
        d[graph[start][j].first] = graph[start][j].second;
    }
    // 시작 노드를 제외한 전체 n - 1개의 노드에 대해 반복
    for (int i = 0; i < n - 1; i++) {
        // 현재 최단 거리가 가장 짧은 노드를 꺼내서, 방문 처리
        int now = getSmallestNode();
        visited[now] = true;
        // 현재 노드와 연결된 다른 노드를 확인
        for (int j = 0; j < graph[now].size(); j++) {
            int cost = d[now] + graph[now][j].second;
            // 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
            if (cost < d[graph[now][j].first]) {
                d[graph[now][j].first] = cost;
            }
        }
    }
}

int main(void) {
    cin >> n >> m >> start;

    // 모든 간선 정보를 입력받기
    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        // a번 노드에서 b번 노드로 가는 비용이 c라는 의미
        graph[a].push_back({b, c});
    }

    // 최단 거리 테이블을 모두 무한으로 초기화
    fill_n(d, 100001, INF);
    
    // 다익스트라 알고리즘을 수행
    dijkstra(start);

    // 모든 노드로 가기 위한 최단 거리를 출력
    for (int i = 1; i <= n; i++) {
        // 도달할 수 X 경우 -> 무한(INFINITY) 출력
        if (d[i] == INF) {
            cout << "INFINITY" << '\n';
        }
        // 도달할 수 O 경우 -> 거리 출력
        else {
            cout << d[i] << '\n';
        }
    }
}

Java

import java.util.*;
class Node {
    private int index;
    private int distance;

    public Node(int index, int distance) {
        this.index = index;
        this.distance = distance;
    }

    public int getIndex() {
        return this.index;
    }

    public int getDistance() {
        return this.distance;
    }
}

public class Main {
    public static final int INF = (int) 1e9; // 무한을 의미하는 값(10억)
    // 노드의 개수(N), 간선의 개수(M), 시작 노드 번호(Start)
    // 노드의 개수: 최대 100,000개 가정
    public static int n, m, start;
    // 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열
    public static ArrayList<ArrayList<Node>> graph = new ArrayList<ArrayList<Node>>();
    // 방문한 적이 있는지 체크하는 목적의 배열 만들기
    public static boolean[] visited = new boolean[100001];
    // 최단 거리 테이블 만들기
    public static int[] d = new int[100001];

    // 방문 X 노드 중에서, 가장 최단 거리가 짧은 노드의 번호를 반환
    public static int getSmallestNode() {
        int min_value = INF;
        int index = 0; // 가장 최단 거리가 짧은 노드(인덱스)
        for (int i = 1; i <= n; i++) {
            if (d[i] < min_value && !visited[i]) {
                min_value = d[i];
                index = i;
            }
        }
        return index;
    }

    public static void dijkstra(int start) {
        // 시작 노드에 대해서 초기화
        d[start] = 0;
        visited[start] = true;
        for (int j = 0; j < graph.get(start).size(); j++) {
            d[graph.get(start).get(j).getIndex()] = graph.get(start).get(j).getDistance();
        }
        // 시작 노드를 제외한 전체 n - 1개의 노드에 대해 반복
        for (int i = 0; i < n - 1; i++) {
            // 현재 최단 거리가 가장 짧은 노드를 꺼내서, 방문 처리
            int now = getSmallestNode();
            visited[now] = true;
            // 현재 노드와 연결된 다른 노드를 확인
            for (int j = 0; j < graph.get(now).size(); j++) {
                int cost = d[now] + graph.get(now).get(j).getDistance();
                // 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
                if (cost < d[graph.get(now).get(j).getIndex()]) {
                    d[graph.get(now).get(j).getIndex()] = cost;
                }
            }
        }
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();
        start = sc.nextInt();

        // 그래프 초기화
        for (int i = 0; i <= n; i++) {
            graph.add(new ArrayList<Node>());
        }

        // 모든 간선 정보를 입력받기
        for (int i = 0; i < m; i++) {
            int a = sc.nextInt();
            int b = sc.nextInt();
            int c = sc.nextInt();
            // a번 노드에서 b번 노드로 가는 비용이 c라는 의미
            graph.get(a).add(new Node(b, c));
        }

        // 최단 거리 테이블을 모두 무한으로 초기화
        Arrays.fill(d, INF);
        
        // 다익스트라 알고리즘을 수행
        dijkstra(start);

        // 모든 노드로 가기 위한 최단 거리를 출력
        for (int i = 1; i <= n; i++) {
            // 도달할 수 X 경우 -> 무한(INFINITY) 출력
            if (d[i] == INF) {
                System.out.println("INFINITY");
            }
            // 도달할 수 O 경우 -> 거리 출력
            else {
                System.out.println(d[i]);
            }
        }
    }
}

---

우선순위 큐(Priority Queue)

• 우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료구조
• ex. 여러 개의 물건 데이터를 자료구조에 넣었다가 가치가 높은 물건 데이터부터 꺼내서 확인해야 하는 경우
• 대부분의 프로그래밍 언어에서 표준 라이브러리 형태로 지원

힙(Heap)

• 우선순위 큐를 구현하기 위해 사용하는 자료구조 중 하나
• 최소 힙(Min Heap)과 최대 힙(Max Heap)
• 다익스트라 최단 경로 알고리즘을 포함해 다양한 알고리즘에서 사용

힙 라이브러리 사용 예제: 최소 힙

import heapq

# 오름차순 힙 정렬(Heap Sort)
def heapsort(iterable):
	h = []
    result = []
    # 모든 원소를 차례대로 힙에 삽입
    for value in iterable:
    	heapq.heappush(h, value)
    # 힙에 삽입된 모든 원소를 차례대로 꺼내어 담기
    for i in range(len(h)):
    	result.append(heapq.heappop(h))
    return result
    
result = heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0])
print(result) # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

최대 힙

import heapq

# 내림차순 힙 정렬(Heap Sort)
def heapsort(iterable):
	h = []
    result = []
    # 모든 원소를 차례대로 힙에 삽입
    for value in iterable:
    	heapq.heappush(h, -value)
    # 힙에 삽입된 모든 원소를 차례대로 꺼내어 담기
    for i in range(len(h)):
    	result.append(-heapq.heappop(h))
    return result
    
result = heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0])
print(result) # [9, 8, 7, 6, 5, 4, 3, 2, 1, 0]

---

다익스트라 알고리즘: 개선된 구현 방법

• 단계마다 방문 X 노드 중 최단 거리가 가장 짧은 노드 선택
  -> 힙(Heap) 자료구조 이용
• 동작하는 기본 원리 동일
  • 현재 가장 가까운 노드를 저장해 놓기 위해 힙 자료구조를 추가적으로 이용한다는 점이 다름
  • 현재의 최단 거리가 가장 짧은 노드 선택 -> 최소 힙 사용

성능 분석

• 시간 복잡도: $O(ElogV)$
• 노드를 하나씩 꺼내 검사하는 반복문(while문)은 노드의 개수 V 이상의 횟수로는 처리 X
  • 결과적으로 현재 우선순위 큐에서 꺼낸 노드와 연결된 다른 노드들을 확인하는 총횟수 
    -> 최대 간선의 개수(E)만큼 연산이 수행될 수 있음
• 직관적으로 전체 과정은 E개의 원소를 우선순위 큐에 넣었다가 모두 빼내는 연산과 매우 유사
  • 시간 복잡도를 $O(ElogE)로 판단할 수 있음
  • 중복 간선을 포함 X 경우 ->  $O(ElogV)$로 정리할 수 있음
    • $O(ElogE)$ -> $O(ElogV^2)$ -> $O(2ElogV)$ -> $O(ElogV)$

Python

import heapq
import sys
input = sys.stdin.readline
INF = int(1e9) # 무한을 의미하는 값(10억)

# 노드의 개수, 간선의 개수를 입력받기
n, m = map(int, input().split())
# 시작 노드 번호를 입력받기
start = int(input())
# 각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트를 만들기
graph = [[] for i in range(n + 1)]
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n + 1)

# 모든 간선 정보를 입력받기
for _ in range(m):
    a, b, c = map(int, input().split())
    # a번 노드에서 b번 노드로 가는 비용이 c라는 의미
    graph[a].append((b, c))

def dijkstra(start):
    q = []
    # 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
    heapq.heappush(q, (0, start))
    distance[start] = 0
    while q: # 큐가 비어있지 않다면
        # 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
        dist, now = heapq.heappop(q)
        # 현재 노드가 이미 처리된 적이 있는 노드라면 무시
        if distance[now] < dist:
            continue
        # 현재 노드와 연결된 다른 인접한 노드들을 확인
        for i in graph[now]:
            cost = dist + i[1]
            # 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
            if cost < distance[i[0]]:
                distance[i[0]] = cost
                heapq.heappush(q, (cost, i[0]))

# 다익스트라 알고리즘을 수행
dijkstra(start)

# 모든 노드로 가기 위한 최단 거리를 출력
for i in range(1, n + 1):
    # 도달할 수 X 경우 -> 무한(INFINITY) 출력
    if distance[i] == INF:
        print("INFINITY")
    # 도달할 수 O 경우 -> 거리 출력
    else:
        print(distance[i])

C++

#include <bits/stdc++.h>
#define INF 1e9 // 무한을 의미하는 값(10억)
using namespace std;

// 노드의 개수(N), 간선의 개수(M), 시작 노드 번호(Start)
// 노드의 개수는 최대 100,000개라고 가정
int n, m, start;
// 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열
vector<pair<int, int> > graph[100001];
// 최단 거리 테이블 만들기
int d[100001];

void dijkstra(int start) {
    priority_queue<pair<int, int> > pq;
    // 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
    pq.push({0, start});
    d[start] = 0;
    while (!pq.empty()) { // 큐가 비어있지 않다면
        // 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
        int dist = -pq.top().first; // 현재 노드까지의 비용 
        int now = pq.top().second; // 현재 노드
        pq.pop();
        // 현재 노드가 이미 처리된 적이 있는 노드라면 무시
        if (d[now] < dist) continue;
        // 현재 노드와 연결된 다른 인접한 노드들을 확인
        for (int i = 0; i < graph[now].size(); i++) {
            int cost = dist + graph[now][i].second;
            // 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
            if (cost < d[graph[now][i].first]) {
                d[graph[now][i].first] = cost;
                pq.push(make_pair(-cost, graph[now][i].first));
            }
        }
    }
}

int main(void) {
    cin >> n >> m >> start;

    // 모든 간선 정보를 입력받기
    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        // a번 노드에서 b번 노드로 가는 비용이 c라는 의미
        graph[a].push_back({b, c});
    }

    // 최단 거리 테이블을 모두 무한으로 초기화
    fill(d, d + 100001, INF);
    
    // 다익스트라 알고리즘을 수행
    dijkstra(start);

    // 모든 노드로 가기 위한 최단 거리를 출력
    for (int i = 1; i <= n; i++) {
        // 도달할 수 X 경우 -> 무한(INFINITY) 출력
        if (d[i] == INF) {
            cout << "INFINITY" << '\n';
        }
        // 도달할 수 O 경우 -> 거리 출력
        else {
            cout << d[i] << '\n';
        }
    }
}

Java

import java.util.*;

class Node implements Comparable<Node> {
    private int index;
    private int distance;

    public Node(int index, int distance) {
        this.index = index;
        this.distance = distance;
    }

    public int getIndex() {
        return this.index;
    }

    public int getDistance() {
        return this.distance;
    }

    // 거리(비용)가 짧은 것이 높은 우선순위를 가지도록 설정
    @Override
    public int compareTo(Node other) {
        if (this.distance < other.distance) {
            return -1;
        }
        return 1;
    }
}

public class Main {
    public static final int INF = (int) 1e9; // 무한을 의미하는 값(10억)
    // 노드의 개수(N), 간선의 개수(M), 시작 노드 번호(Start)
    // 노드의 개수: 최대 100,000개 가정
    public static int n, m, start;
    // 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열
    public static ArrayList<ArrayList<Node>> graph = new ArrayList<ArrayList<Node>>();
    // 최단 거리 테이블 만들기
    public static int[] d = new int[100001];

    public static void dijkstra(int start) {
        PriorityQueue<Node> pq = new PriorityQueue<>();
        // 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
        pq.offer(new Node(start, 0));
        d[start] = 0;
        while(!pq.isEmpty()) { // 큐가 비어있지 않다면
            // 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
            Node node = pq.poll();
            int dist = node.getDistance(); // 현재 노드까지의 비용 
            int now = node.getIndex(); // 현재 노드
            // 현재 노드가 이미 처리된 적이 있는 노드라면 무시
            if (d[now] < dist) continue;
            // 현재 노드와 연결된 다른 인접한 노드들을 확인
            for (int i = 0; i < graph.get(now).size(); i++) {
                int cost = d[now] + graph.get(now).get(i).getDistance();
                // 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
                if (cost < d[graph.get(now).get(i).getIndex()]) {
                    d[graph.get(now).get(i).getIndex()] = cost;
                    pq.offer(new Node(graph.get(now).get(i).getIndex(), cost));
                }
            }
        }
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();
        start = sc.nextInt();

        // 그래프 초기화
        for (int i = 0; i <= n; i++) {
            graph.add(new ArrayList<Node>());
        }
        
        // 모든 간선 정보를 입력받기
        for (int i = 0; i < m; i++) {
            int a = sc.nextInt();
            int b = sc.nextInt();
            int c = sc.nextInt();
            // a번 노드에서 b번 노드로 가는 비용이 c라는 의미
            graph.get(a).add(new Node(b, c));
        }

        // 최단 거리 테이블을 모두 무한으로 초기화
        Arrays.fill(d, INF);
        
        // 다익스트라 알고리즘을 수행
        dijkstra(start);

        // 모든 노드로 가기 위한 최단 거리를 출력
        for (int i = 1; i <= n; i++) {
            // 도달할 수 X 경우 -> 무한(INFINITY) 출력
            if (d[i] == INF) {
                System.out.println("INFINITY");
            }
            // 도달할 수 O 경우 -> 거리 출력
            else {
                System.out.println(d[i]);
            }
        }
    }
}

---

플로이드 워셜(Floyd-Warshall) 알고리즘

• 모든 노드에서 다른 모든 노드까지의 최단 경로 모두 계산
• 다익스트라 알고리즘과 마찬가지로 단계별로 거쳐 가는 노드를 기준으로 알고리즘 수행
  • 다만 매 단계마다 방문 X 노드 중 최단 거리를 갖는 노드를 찾는 과정 필요 X
• 2차원 테이블에 최단 거리 정보 저장
• 다이나믹 프로그래밍 유형에 속함

 

• 각 단계마다 특정한 노드 k를 거쳐 가는 경우 확인
  • a에서 b로 가는 최단 거리보다 a에서 k를 거쳐 b로 가는 거리가 더 짧은지 검사
• 점화식
  • $D_{ab} = min(D_{ab}, D_{ak} + D_{kb})$

성능 분석

• 노드의 개수가 N개 일 때 알고리즘상으로 N번의 단계를 수행
  • 각 단계마다 $O(N^2)$의 연산 ~> 현재 노드를 거쳐 가는 모든 경로를 고려
• => 총 시간 복잡도 $O(N^3)$

Python

INF = int(1e9) # 무한을 의미하는 값(10억)

# 노드의 개수 및 간선의 개수 입력받기
n = int(input())
m = int(input())
# 2차원 리스트(그래프 표현) 만들고, 무한으로 초기화
graph = [[INF] * (n + 1) for _ in range(n + 1)]

# 자기 자신 -> 자기 자신 => 비용: 0으로 초기화
for a in range(1, n + 1):
	for b in range(1, n + 1):
    	if a == b:
        	graph[a][b] = 0
            
# 각 간선에 대한 정보 입력 받아, 그 값으로 초기화
for _ in range(m):
	# A에서 B로 가는 비용: C라고 설정
    a, b, c = map(int, input().split())
    graph[a][b] = c
    
# 점화식에 따라 플로이드 워셜 알고리즘 수행
for k in range(1, n + 1):
	for a in range(1, n + 1):
    	for b in range(1, n + 1):
        	graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
            
# 수행된 결과 출력
for a in range(1, n + 1):
	for b in range(1, n + 1):
    	# 도달할 수 X 경우 -> 무한(INFINITY)라고 출력
        if graph[a][b] == INF:
        	print("INFINITY", end=" ")
        else:
        	print(graph[a][b], end=" ")
    print()

C++

#include <bits/stdc++.h>
#define INF 1e9 // 무한을 의미하는 값(10억)
using namespace std;

// 노드의 개수(N), 간선의 개수(M)
// 노드의 개수: 최대 500개 가정
int n, m;
// 2차원 배열(그래프 표현)를 만들기
int graph[501][501];

int main(void) {
    cin >> n >> m;

    // 최단 거리 테이블을 모두 무한으로 초기화
    for (int i = 0; i < 501; i++) {
        fill(graph[i], graph[i] + 501, INF);
    }

    // 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
    for (int a = 1; a <= n; a++) {
        for (int b = 1; b <= n; b++) {
            if (a == b) graph[a][b] = 0;
        }
    }

    // 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
    for (int i = 0; i < m; i++) {
        // A에서 B로 가는 비용은 C라고 설정
        int a, b, c;
        cin >> a >> b >> c;
        graph[a][b] = c;
    }
    
    // 점화식에 따라 플로이드 워셜 알고리즘을 수행
    for (int k = 1; k <= n; k++) {
        for (int a = 1; a <= n; a++) {
            for (int b = 1; b <= n; b++) {
                graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b]);
            }
        }
    }

    // 수행된 결과를 출력
    for (int a = 1; a <= n; a++) {
        for (int b = 1; b <= n; b++) {
            // 도달할 수 X 경우 -> 무한(INFINITY) 출력
            if (graph[a][b] == INF) {
                cout << "INFINITY" << ' ';
            }
            // 도달할 수 O 경우 -> 거리 출력
            else {
                cout << graph[a][b] << ' ';
            }
        }
        cout << '\n';
    }
}

Java

import java.util.*;

public class Main {
    public static final int INF = (int) 1e9; // 무한을 의미하는 값(10억)
    // 노드의 개수(N), 간선의 개수(M)
    // 노드의 개수: 최대 500개 가정
    public static int n, m;
    // 2차원 배열(그래프 표현)를 만들기
    public static int[][] graph = new int[501][501];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();

        // 최단 거리 테이블을 모두 무한으로 초기화
        for (int i = 0; i < 501; i++) {
            Arrays.fill(graph[i], INF);
        }

        // 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
        for (int a = 1; a <= n; a++) {
            for (int b = 1; b <= n; b++) {
                if (a == b) graph[a][b] = 0;
            }
        }

        // 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
        for (int i = 0; i < m; i++) {
            // A에서 B로 가는 비용은 C라고 설정
            int a = sc.nextInt();
            int b = sc.nextInt();
            int c = sc.nextInt();
            graph[a][b] = c;
        }

        // 점화식에 따라 플로이드 워셜 알고리즘을 수행
        for (int k = 1; k <= n; k++) {
            for (int a = 1; a <= n; a++) {
                for (int b = 1; b <= n; b++) {
                    graph[a][b] = Math.min(graph[a][b], graph[a][k] + graph[k][b]);
                }
            }
        }

        // 수행된 결과를 출력
        for (int a = 1; a <= n; a++) {
            for (int b = 1; b <= n; b++) {
                // 도달할 수 X 경우 -> 무한(INFINITY) 출력
                if (graph[a][b] == INF) {
                    System.out.print("INFINITY ");
                }
                // 도달할 수 O 경우 -> 거리 출력
                else {
                    System.out.print(graph[a][b] + " ");
                }
            }
            System.out.println();
        }
    }
}

---